Noiseless Searching Keys: an Algorithmic Adventure

tl;dr: implementation and explanation of a solution for one of my projects. The half-polished code of LeakSolver can be found here. What follows lives in the intersection of this freebie and this other freebie.

Searching Solutions by Writing Code

Imagine the most typical scenario in side-channel attacks: an AES-128 (AES from now on) encryption process where the attacker gains access to the Hamming weight of the sbox-outputs. This scenario is quite widespread, so I’m introducing a unique twist: noiseless leaks and access to leaks from the first two rounds only.

Given a single message and the related leaks, how many keys might be viable key-candidates? Is it feasible to compute these within a reasonable time? This presents an intriguing cryptanalysis challenge, so let’s delve deeper into it!

Unrolling (a bit of) AES

Before moving into the problem, let me unroll the first two rounds of AES.¹ As a nice clarity-companion, let me share a picture of all this big mess!²

First-ish round unrolled AES. Above, the key scheduler's actions to obtain the first expanded key. Under, the common AES round actions.

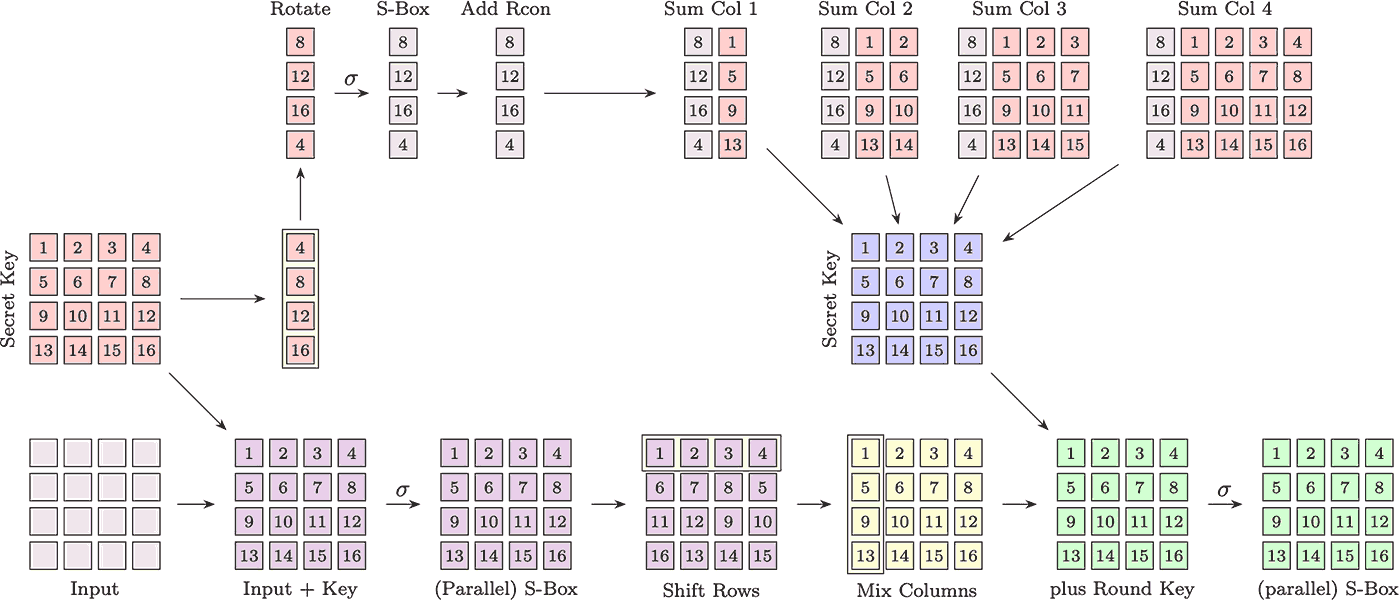
AES operates as a substitution-permutation block cipher, taking fixed-length input and incorporating a secret key. The input is organized into a 4x4 grid of bytes, forming the current message state. Each cell of this grid undergoes independent permutation using the AES permutation function. Following this, a linear action is performed on the grid, which includes row shifting and column mixing.

Meanwhile³,the secret key undergoes expansion. It’s conceptualized as another 4x4 grid state. The last column undergoes rotation, each element is permuted using the AES permutation function and a constant value is (sometimes) added. This computed column is then added to the first column of the secret key to get the first column of the new round key. Then, this first new column is added to the second-old columns and the process repeats until the last (fourth) column is computed, creating the subsequent secret round key.

Finally, the message state and the new round key are combined, initiating the next AES round. This involves computing the AES permutation on each cell within the message state.

Exploiting the Independency

Picture this: the adversary selects an input $x$ and requests its AES encryption, aiming to gather information from the device’s computations. The device, holding a secret key $k$, encrypts $x$ and leaks the Hamming weight (i.e. the number of ones) of all the AES permutations (s-boxes) in the initial two rounds.

As evident from the preceding illustration, the s-boxes of the first round depend solely on one segment of the secret key, referred to as the subkey. Having knowledge of the input and the precise count of ones in the s-box output proves particularly advantageous in retrieving the subkey. For instance, a weight of $0$ signifies that the s-box output is hexadecimal $00$, corresponding to the hexadecimal input $52$. Given the input, retrieving the subkey is straightforward: $k_i = 52 \oplus x_i$. However, if the weight is $1$, there exist $8$ potential outputs, leading to $8$ possible subkey guesses. Generally, if the weight is $i$, there are $\binom{8}{i}$ feasible guesses. The correct guess lies within that list, yet we lack the means to differentiate it.

We can potentially do the same for the second round!⁴ However, the calculated guesses rely on numerous subkeys, as both the round key and the current state are derived from computing the key scheduler and the round function. These computations depend on several subkeys and let me show you the dependencies of the second s-box outputs and the original secret key subkeys.

Dependencies between the second round s-boxes and the secret subkey. For practicality, the colours are related to the previously unrolled AES diagram.

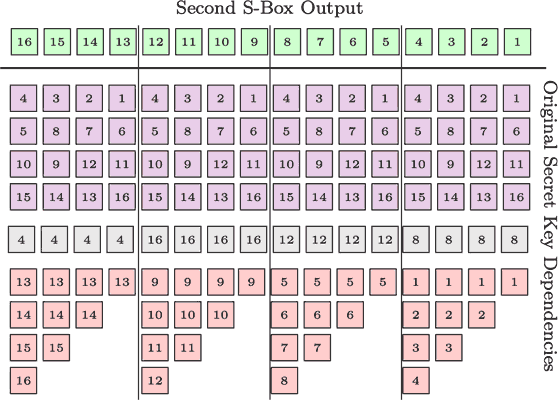
As the curious reader might notice, each second-round output does not depend on the whole secret key, some of them are either independent of each other or have minor differences. For example, the first byte only depends on the $(1,6,11,16,8)$-th subkeys meaning that we can obtain the candidates for such positions and additionally verify if they correctly combine as a possible second round first byte guess. If we get a good candidate for the first byte, we can consider the ninth byte which depends on $(1,6,11,16,9)$-th subkeys. Observe that we only check the $9$-th subkey’s candidate since the others are already “fixed” by the previous guess.

If we take as next byte to guess the one that minimizes the “new subkey dependencies”, we cleverly navigate a tree structure with some conditional checks that allow to skip whole big branches. This is exactly what my other project IndexTree does: it traverses a big-tree containing all the possible subkey candidates but allows skipping whole branches if some of the second-round conditions are not achieved.

In summary, we cleverly sort the second-round check to minimize the additional dependencies, we start navigating the candidates in IndexTree and, whenever a second-round condition fails, we skip the whole subtree thus diminishing the candidates to check.⁵

Run the Crustacean

As you might guess, I fully implemented the solver LeakSolver in Rust and you can find the code in this repo. Despite I already presented some speed arguments in this other post, I want to show the limits of such a solver or, in other words, until when the solver is reasonably efficient on my old MacBook Pro⁶ while running in the background!

For the sake of simplicity, my experiment will consider the input to be random and it will randomly sample a secret key, generate the problem and solve it. I will record the execution time and something ⁷ related to the Hamming weight of the whole random secret key to allow some discrimination between the keys.

Well, the first thing to find out is if the solver can solve the problem with a random secret key in a reasonable amount of time! So, the first run gave me this timing of “too much time, try something easier” which I promptly replied with a “taking a deep breath”. The main problem of taking everything at random is that with high probability one gets into an enormous set of candidates and, as an additional problem, not all the same weight subkeys are the same.

To solve this and to get some plots, I decided to manually construct the keys with a desired weight and looked into the time and problem hardness distribution. Since I’m unable to properly get a sample of the timing for all the possible weights, I plotted the special Hamming weight distribution for uniform random keys.

Timing box-plots depending on the special Hamming weight of the first s-box output. On the right, the number of solutions found for the first s-box output's Hamming weight.

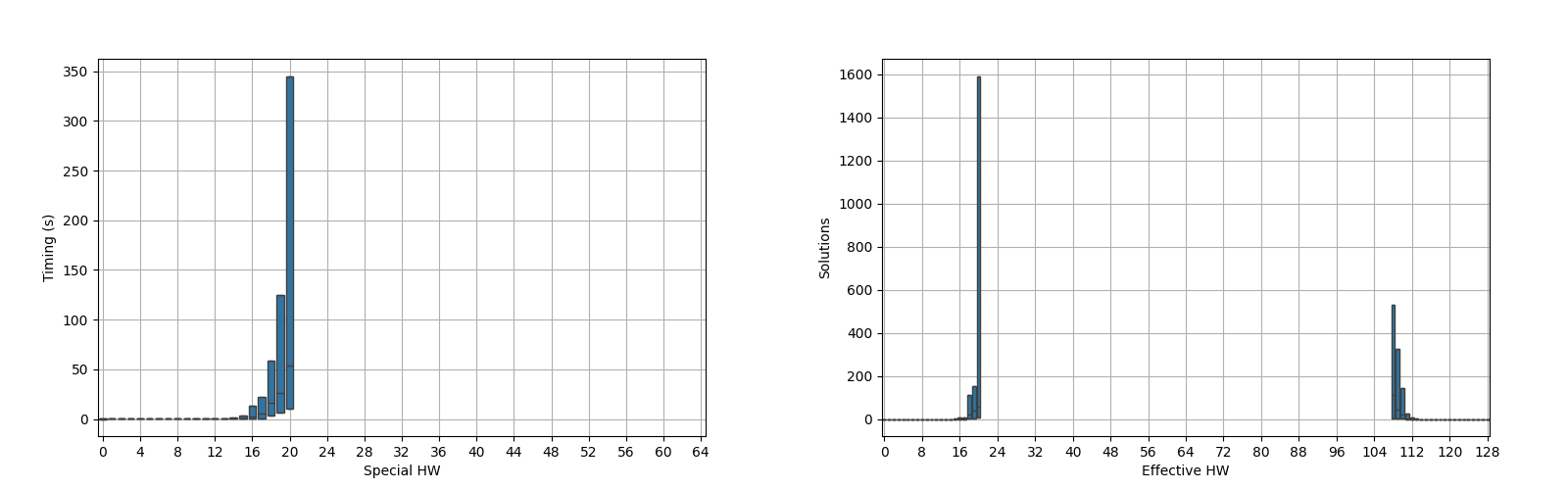
First, it is nice to see that the special⁷ Hamming weight of the first s-box output is a good measurement for timing estimation. If one remembers the unrolled AES diagram, it should be clear that the first outputs are the sole responsible to the amount of (sub)key candidates: if many weights are $0$ or $8$, then many subkey candidates are unique however these candidates might have any weight because of the s-box permutation action that modifies the weights.

As expected, the timing exponentially flies out of orbit making it definitely hard to fully analyse harder keys. Following the IndexTree post, technically I can generate keys with a special Hamming weight of ~40 however these might not be that representative of the space. These keys are distributed as six subkeys with a weight of $0$ and the remaining with a weight of $4$ thus $6 \cdot 0 + 10 \cdot 4 = 40$. However, a quick check points out that a random key has more variety, like $0 \cdot 0 + 3 \cdot 1 + 5\cdot 2 + 5\cdot 3 + 3\cdot 4 = 40$ which takes an undisclosed amount of time.

To answer the initial question, the number of keys explodes and what I got is barely what I would call a reasonable amount of time. It is funny to notice how small the solution set is with respect to the whole candidate sets: for Hamming weight $20$, one can get an average of $28^{5} = 17\,210\,368$ candidates and an average solution set of $~70$ keys which are the $0.000407\%$ of the whole candidate space. Even the reasonable (according to Python) maximum of $1600$ candidates is the $~0.01\%$! Adding the leaks for the second round of s-boxes massively reduces the candidate set cardinality!

Take Away

Here is a mix of improvements, future questions, directions and thoughts:

• Easy Improvements for LeakSolver: the easiest way to fill up some of the missing entries in the plots is to improve the code by cleaning up some of the logic to make it more straightforward, moving fewer references and revisiting some code choices I made.⁸ I suspect that with some easy clean up, I can reach keys with ~20 special HW. Still, a lot to do but it is better than nothing!

• Weird-Easy Improvements for LeakSolver: it would be cool to execute the tree navigation differently: instead of taking a branch and checking all the possible leaves, it might be cool to only verify the number of branches that require further checks. Basically, extract all the good candidates that are good for the first check which already provides a better idea of the effective dimensionality of the problem. In my mind, this way would not modify the amount of checks executed but it would provide a more reasonable feedback via a progress bar when executing. Currently, the progress bar highlights the current candidate with respect to the total amount. The modified version would start by pointing out which level we are currently in and how many branches are done for that specific level.

  Now that I have written down the improvement, I realise that this can somehow-easily be done by visualising the IndexTree current index in some clever way.

• Hard Improvements for LeakSolver: an additional trick that moves some computational cost into memory is to keep track of the inputs of failing conditions down the tree. The main reason is that any specific combination might reappear in another branch because of how the indices are distributed in the checks. In theory, this makes sense. In practice, this might explode since it requires executing a membership test of an increasing list for each candidate and, eventually, computing the verification predicate regardless. Maybe this idea can be used in a different way?

• Hard-Hard Improvements for LeakSolver: in theory, the IndexTree navigation can be done in parallel: different branches are fully navigated by different processes which either push a key candidate or skip to the next branch. This can definitely be done in Rust. However, I’m not fully sure how hard it would be to implement and if this would effectively provide any major gain.

• AES-192 and AES-256: I would like to extend LeakSolver to work for AES-192 and AES-256 too. The main difference here is the key scheduler: the blockcipher is still operating on 128 bits thus the additional 64/128 bits of the secret key are pushed into the first round key. This modifies the whole diagram, the dependencies, the order of the checks and the whole IndexTree structure. It mainly takes some time to do these computations and, personally, it might be better to first get a general enough solver with an easy interface that programmatically handles these conditions so that the only thing I must provide is the list of indices and checks to do.

• SKINNY: similar to before, I would like to get my hands on a small blockcipher too. Skinny is a 64-bit blockcipher with a peculiar structure that “doesn’t mix too much” the secret key in the first rounds. My goal would be to get LeakSolver to solve a random instance of Skinny in a reasonable amount of time. Let’s say… 5-10 minutes!

• Reality of Side-Channel Attack: to throw another stone: common SCA divide-et-impera gives each subkey $k_i$ guess a probability $p_i$ based on the real measurement and the possible leak coming from a model. An assumption made is that the subkeys are independent so the whole candidate key $(k_i)$ is the correct guess with probability $\prod p_i$. How can we refine by adding the second round of leaks? Fixed a candidate key, this will completely determine the second round of leaks thus providing another layer of probabilities to distinguish between more/less probable candidates. What if we fix a list of leaks which will give us some probability and later check which keys respect this choice?

  There are some opportunities for improving attacks but one might be require to do the math and see “how and when” the approach makes sense.

Footnotes